The Simplest School Math Puzzle That College Students Couldn't Solve!
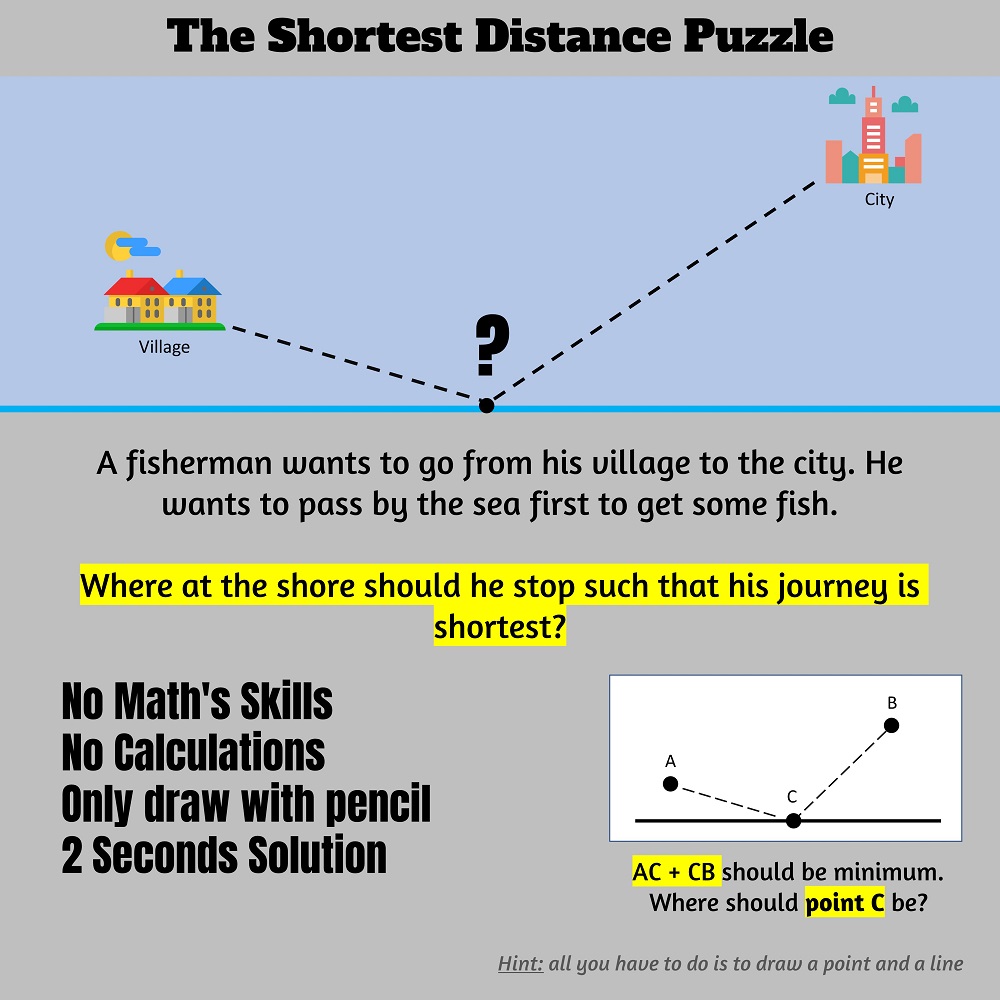
I have shown this simple puzzle to more than a dozen of math college students and almost no one managed to figure out the solution.
The puzzle is secondary school level yet most people struggle with it.
The puzzle is by no means difficult to solve. As a matter of fact, there are a least three different ways to find the shortest path.
The requirement however is to solve it without calculations and without using advanced math techniques whatsoever.
Also, the solution must be demonstratable in no more than 5 seconds with only drawing a point and line.
I highly encourage you to try to solve it yourself before you see the solution below. The concept is extremely simple and elementary.
The solution:
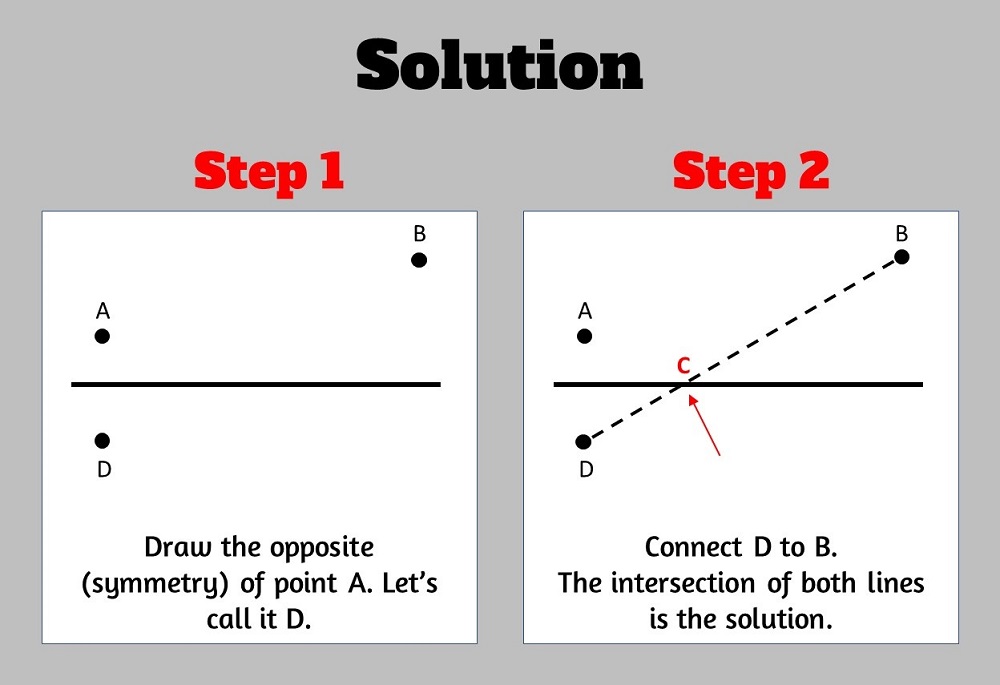
Step One:
Take the symmetry (opposite) of point A.
The symmetry is at the same distance from the line as point A but from the other side.
Let us call this new point D.
Step Two:
Connect point D with point B. The two lines will intersect at point C, the point we are looking for.
Why is this the shortest route?

Because point D is the opposite of point A, then it is at the same distance to any point on the line, so can scrap point A and just focus on point D since it is the same distance.
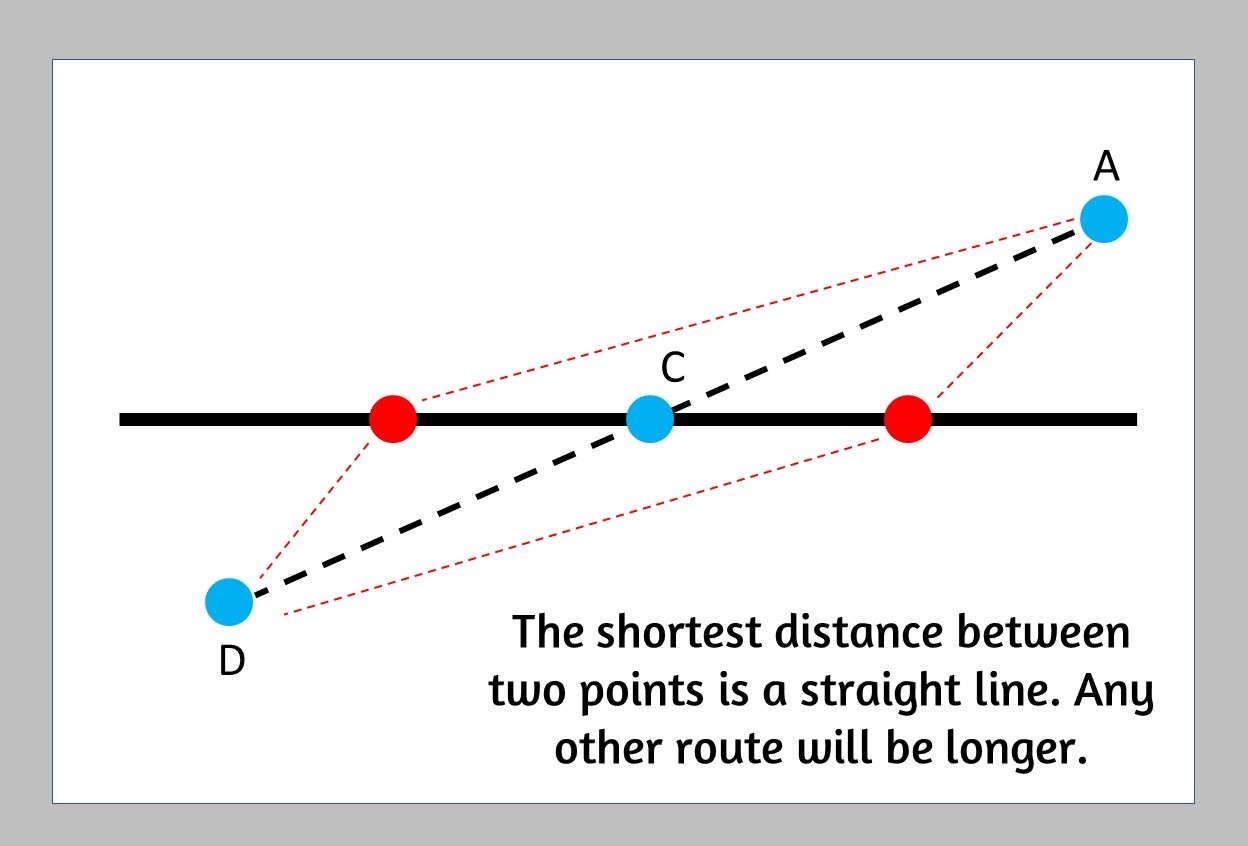
The shortest distance between two points is a straight line
Connecting D and B will give us the shortest path. If you draw any other path you will quickly find out that it is longer.
 Close
Close



 FEED
FEED JOIN
JOIN MONETIZATION
MONETIZATION HELP
HELP LOGIN
LOGIN













